This meansthat we could construct a man (meaning his neuronic nervous system)using electronic circuits and an awareness device. But how could we attach awareness (i.e. beingness) to the electronic network ? We should first know how is awareness attached to the neurons network and only then attempt to "attach" it to an electronic network. We could not imagine beingness only as an epiphenomenon, but influencing the nervous automaton. The internal device for reorganizing the incomplete automaton (Fig.43) could also engulf the effect of human awareness.
Any decomposition of an automaton into several automata leads to a system of automata. The part maintaining contact with the external world (Fig. 42) is not necessary a deterministic automaton, it could also be stochastic. In general we could have a system of very complex automata, but always the system ofautomata will be equivalent to a single automaton³⁴. In other words, a system of automata is an automaton. Therefore, were man an automaton, then society would be an automaton too³⁵. But it is sufficient that only one element be not a mere automaton, but more than that, for the whole structure to be (at least potentially) more than an automaton.

7. A stochastic automaton with finite states is defined³⁶ as a machine m = <X, Y, S, p(y, s'/s,x)> (5) and a probability distribution following the states P = P(s) (6). Inexpression (5), X, Y, and S have the same significance as previously,i.e. X is the input alphabet, Y is the output alphabet, and S is the set of states. While p(y, s'/s,x) (7) is the probability that for an input x and an initial state s,the outputbecomes y and the state s'. For p = 0 or p = 1 one gets a deterministic automaton. The initial state of a deterministic automaton is not generally known, but only the probability distribution (6) of such a state. Hence the most general form of a stochastic automaton is the couple = (m,p) (8).

If we knew the initial state then we would get stochastic automaton = (m, s)(9). The change from a state s to other states is stochastic and it is subject to a probability distribution function according to states. Similarly, the transition to a new output y for an input x. If the transition from a states to a state s' is deterministic,then only the appearance of the output y remains stochastic. One notices that between the most general stochastic automaton and the deterministic automaton there are several other types. But this is not of interest here since we are looking for a global understanding of stochastic automata.
The relevant fact is that there is a "machine" (algorithm, programme, etc, either physically existent or just imagined) that is subject to probability distribution. Then consider the automaton to be in an initial state defined by a probability distribution and assume a sequence x₁x₂x₃x₄x₅ is applied at its input end. After x₁ a new probability distribution is obtained at the output end, which is changed again by x₂ and so on. Finally there is a certain probability of obtaining at the output a sequence y₁y₅y₁₇y₂₀y₂₁ , and an other probability of obtaining y₂y₃y₄y₅y₇ .Now we could look at things in two different ways:

1. What couldmake the automaton concentrate its probability distributionsand to give the output to an input x₁x₂x₃x₄x₅ in a narrower band of possibilities ? We are thinking of something similar to the case in which the sequence x₁x₂x₃x₄x₅ had a special significance in its memory following some learning (or self-learning) process;
2. If the probability distributions were very unfocused, then to what extend could a certain output sequence be identified as due to the automaton functioning.

In the automata theory a significant importance is given to the input and output sequences; certain equivalences between automata are established based on these equivalences and finally minimal automata are established, including stochastic ones. The two ways of approach presented above raise the question of significance of sequences, of their semantic contents, but also of the problem of self-learning and of creation.
Regarding creation we should observe the difference between the case we examined in connection with Fig. 43, and the way we see things now considering an heuristic creation based on language: we consider a given output alphabet and then note that it is only a potentiality that a letter combination at the output will be able to bring heuristically a result of new significance. The control automaton of a stochastic automaton (Fig. 44) could have the property of given significances according to its learning or self-learning, and thus include also heuristic results. It follows that a certain automaton semantic can be considered, a semantic without living, as resulting from the inscription in memory of the results of repeated contacts with the environment thus resulting in a data bank of specific significances.

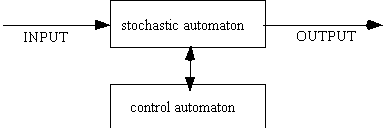
Fig. 44

Regarding the learning and self-learning automata, their study has developed quite a lot , especially in connection with shape and letter recognition³⁷. An automaton for shape recognition will have a learning phase, quite long, and then an operational phase, of classifying the shapes it meets. The recognition of geometrical shapes, including alphanumerical ones, is based on their algebrization, on transforming them in a sequence of 1 and 0. Consider for example the letter A in a lattice of 225 little squares (Fig. 45); then a 225-vector will be written having 1 for the black squares and 0 for the white ones. And to letter B an other 225-vector will be formed and so on. The processing of these algebraic vectors forms the learning of the automaton in letter recognition. Other algebrization methods also exist, some leading to the possibility of recognizing hand writing. However we underline the discrete algebraic treatment of shapes and characters.

Fig. 45

---

Intro-Open Systems 80