Hence, any such existence begins with time. Time itself begins "to flow" as soon as such an existence emerges. This time "flow" incorporates all the subtletieswhich the scientific notion of time may cover. Hence, t = -infinite does not exist.
As concerns t = +infinite, let us observe that once a space-time existence has been triggered off, it goes on developing and we may devise models under which this evolution (motion) should be endless.
In the case illustrated in Fig. 52, space-time existence would vanish gradually towards +infinite. In the case given in Fig. 53, it would grow continually, whereas in Fig. 54 the growth of existence would cease towards +infinite, being then almost constant.
In order to examine these images, let us first observe that by virtue of assumption (XIII) we have assigned an invariant to the world. In a simplified formulation, we say that the sum of existence plus orthoexistence should be constant. In cases (a), (b), and (c), orthoexistence changes partially into space-time existence beginning from t = 0. If a conservation principle holds, then case (b) must be rejected because the change of orthoexistence into a space-time existence is subject to no restriction. Nor could an endless restriction be admitted since this would deny the most general principle of motion under which the existence-orthoexistence change one into another. If the entire orthoexistence would have been transformed into a space-time existence at t = 0 in case (c), then the orthoexistence would only have been found again at t = +infinite, which means that it would have never been found again. This is tantamount to saying that the aim of orthoexistence would be to bring forth existence for good, and as soon as this happened, orthoexistence would vanish. This appears to be unconceivable. Like that form of existence , which has space and time as coordinates, so might orthoexistence have its own coordinates, which will be briefly referred to as the coordinates of orthoexistence. The thorough change of orthoexistence into existence can be conceived, but an endless vanishing of orthoexistence and of its own coordinates would be inconceivable indeed.
Cases (a) and (a'), which are the last to be examined, would imply that t = +infinite. However, at least for reasons of symmetry, to which physical justifications may be found, we cannot refute t = -infinite and admit t = +infinite.That is why any space-time existence is against its own finitetime.



Fig. 52



Fig. 53



Fig. 54

In a distinct image, we might represent a synthetical coordinate of orthoexistence as "supplementary" to space and time (Fig. 55). A like image springs from the manner in which we understand things nowadays and might become a highly unfaithful model of reality. A more accurate way to describe orthoexistence might be entirely different, and so might the orthoexistence-existence connections be. Nevertheless, we shall resort to the model illustrated in Fig. 4a as it is beginning to draw the attention of contemporary physicists and philosophers. Such a model suggests that two, or even more, existences with their associated time and space (Fig. 55b) might spring from orthoexistence. So, there might exist hosts of existences, which could not however be found within the same space, i.e. in the sense of space-time existence. So far, we do not yet know whether these existences are likely to be in touch with another, or whether one could transgress the space and time of our existence. In case any intercourse between existences is precluded, we do not know whether a certain coupling via orthoexistence is not likely to work. If such a coupling exists, the conservation principle would then be valid for orthoexistence and for the entire host of existences. Of course, the "laws of nature " would then differ from one space-time existenceto another.
The universal motion of the total existence, which is formulated in principle (XIII), is the ground to admit some evolutions of space-time existences. Additionally, no space-time existence will come to t = ±infinite. A space-time existence unfolds each time against its own time, which is always finite.

However, is the world compatible with t =±infinite? The answer is both yes and no. First,let us note that we do not know what time means outside space-time existence. From the finite time of such a given existence, and knowing that there are also other space-time existences which may appear to be preceding or successive, the world may appear as having an infinite time.



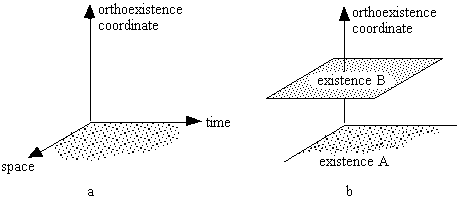
Fig. 55

We extrapolate the time of our existence with respect to the existence of our universe, and know that outside this time (which exists as long as this existence) there exist, or there will exist, other experiences, and hence from this standpoint we may say that the world is infinite in time ( from t = -infinite to t = +infinite). That is why we could state that the world is infinite or finite in time (XIV).

The Philosophical Experiment 89